P value
-
# p-values_simulation approach.R
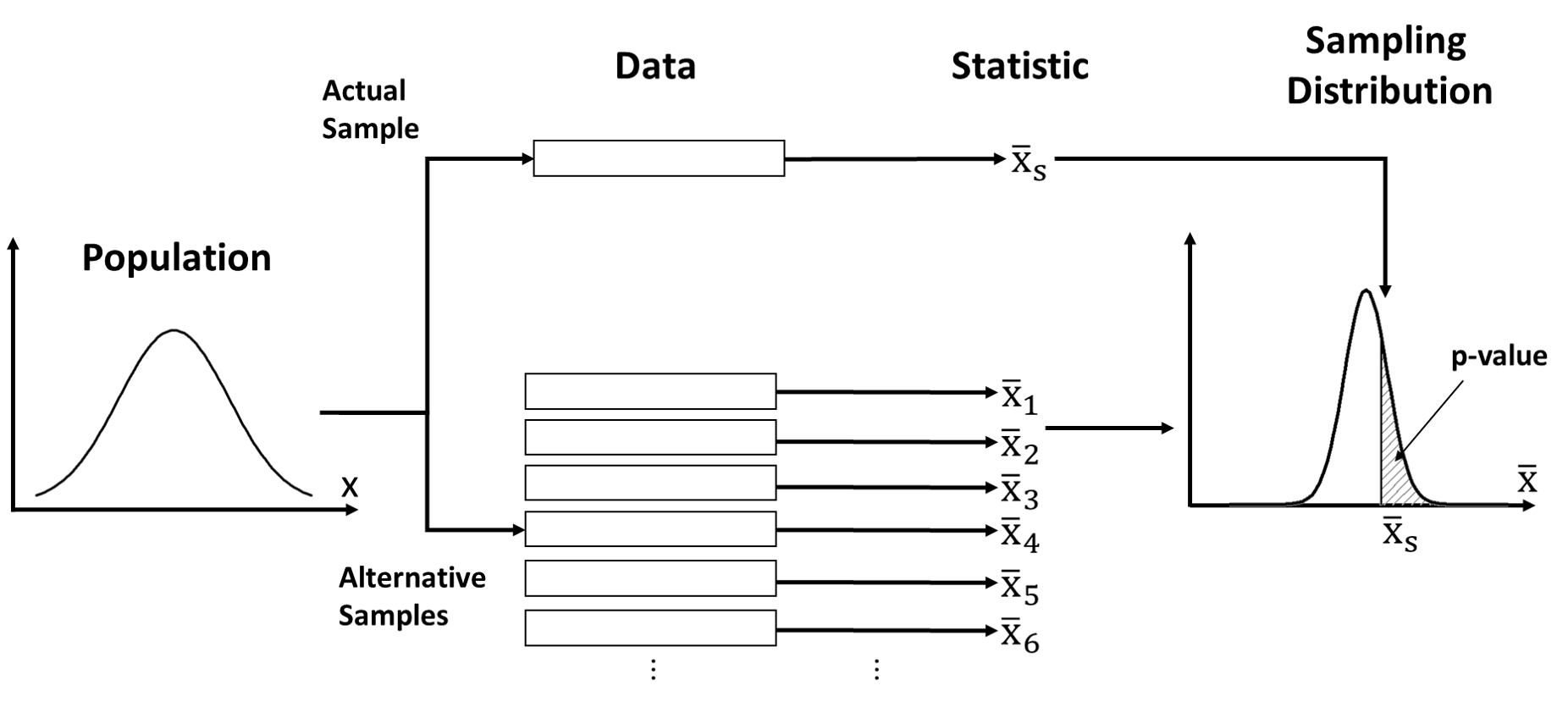
# Where do p-values come from? Fundamental concepts and simulation approach
# https://alemorales.info/post/introduction-sampling-distribution/
sample = c(1.52, 5.24, -0.23, 2.47, 2.63)
for(lib in c("furrr", "distr6")) {
library(lib, character.only = TRUE)
}
plan(multiprocess)
set.seed(2019)
sigma_hat = sd(sample)
mu = 0
population = Normal$new(mean = mu, sd = sigma_hat)
calc_statistic = function(x, mu0 = 0) {
(mean(x) - mu0)/(sd(x)/sqrt(length(x)))
}
N = 5e4
sampling_distribution = future_map_dbl(1:N, ~ calc_statistic(population$rand(5)))
plot(density(sampling_distribution,),
xlab = "t statistic", main = "",
xlim = c(-10,10)) # Histogram of sampling_distribution
curve(dt(x,4), -10, 10, add = T, col = 2, n = 1e3) # Theoretical distribution t(n-1)
abline(v = calc_statistic(sample), col = 3) # Observed statistic
sum(sampling_distribution >= calc_statistic(sample))/N
1 - pt(calc_statistic(sample), 4)
t.test(sample, alternative = "greater")$p.val
N = 5e4
sampling_distribution = future_map_dbl(1:N, ~ mean(population$rand(5)))
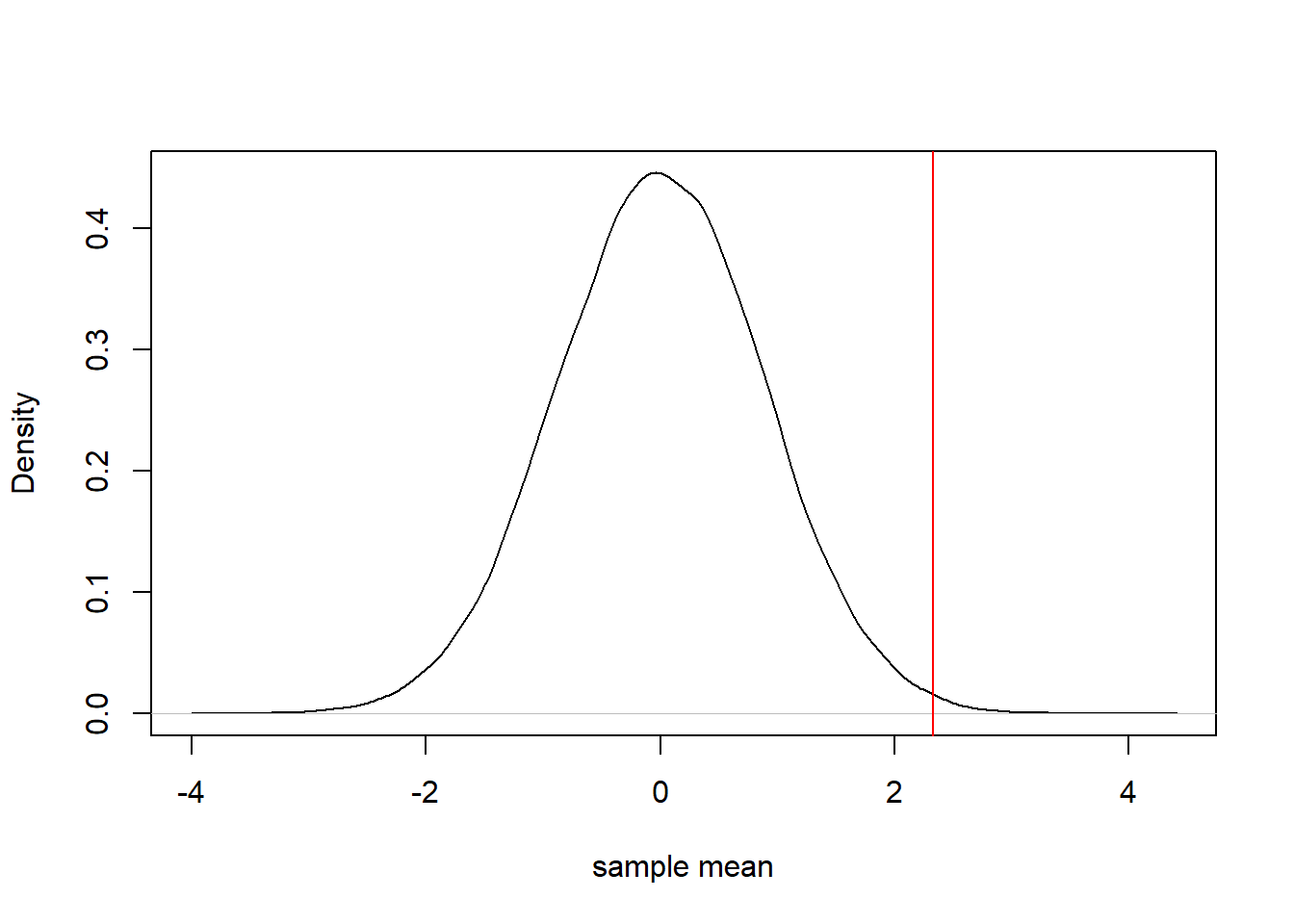
plot(density(sampling_distribution, bw = "SJ"), main = "", xlab = "sample mean") # Histogram of sampling_distribution
abline(v = mean(sample), col = 2) # Observed statistic
sum(sampling_distribution >= mean(sample))/N
-

-
Reference


