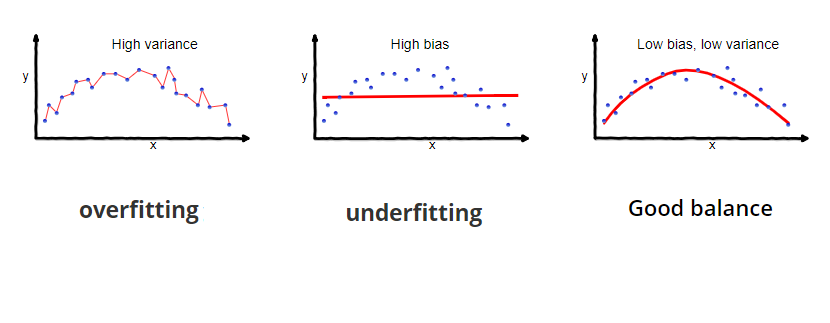
bias-variance tradeoff

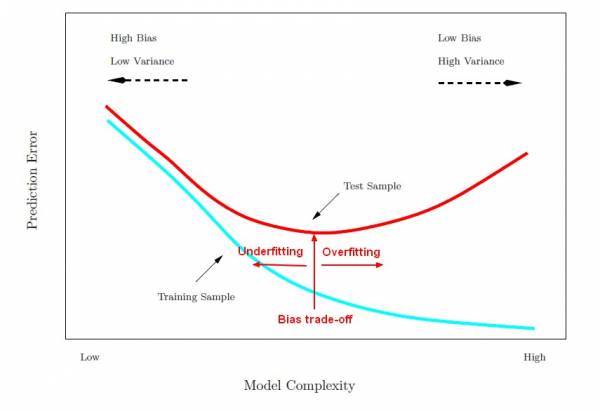from: Statistics - Bias-variance trade-off (between overfitting and underfitting) [Gerardnico]

* 低偏差的model在訓練集合上更加準確，
* 低變異的model在不同的訓練集合上性能更加穩定。

舉兩個極端的例子：

* 記住訓練集合上所有data的label，這樣的系統是低偏差、高變異。(overfitting)
* 無論輸入什麼data，總是預測一個相同的label，這樣的系統是高偏差、低變異。(underfitting)
  • training and testing error curves as a function of training set size
    • will potentially inform us about whether the model has a bias or variance problem and give clues about what to do about it.

    • If the model has a bias problem (underfitting)
      • then both the testing and training error curves will plateau quickly and remain high.
      • This implies that getting more data will not help! We can improve model performance by reducing regularization and/or by using an algorithm capable of learning more complex hypothesis functions.
    • If the model has a variance problem (overfitting)
      • the training error curve will remain well below the testing error and may not plateau.
      • If the training curve does not plateau, this suggests that collecting more data will improve model performance.
      • To prevent overfitting and bring the curves closer to one another, one should
        • increase the severity of regularization,
        • reduce the number of features
        • and/or use an algorithm that can only fit simpler hypothesis functions.

from: Overfitting, bias-variance and learning curves - rmartinshort

  • training and testing error vs model complexity
    • provides a good illustration of the tradeoff between underfitting and overfitting

Reference:

results matching ""

    No results matching ""